Trigonometri merupakan salah satu cabang penting di bidang ilmu matematika. Mereka berhubungan erat dengan sudut dan panjang sisi dalam segitiga, terutama segitiga siku-siku. Meski awalnya terlihat rumit, rumus trigonometri sebenarnya cukup mudah untuk kita pahami. Terutama jika mempelajarinya secara bertahap dan sungguh-sungguh.
Mengenal Apa Itu Rumus Trigonometri
Secara etimologis, kata “trigonometri” berasal dari bahasa Yunani. Mencakup “trigonon” berarti “tiga sudut”, dan metron yang artinya “pengukuran”. Jadi, secara sederhana ini adalah ilmu yang mempelajari hubungan antara sudut dan panjang sisi dalam segitiga.
Fokus utama trigonometri adalah tiga fungsi utama, yaitu sinus (sin), cosinus (cos), dan tangen (tan). Ketiganya berfungsi untuk mencari perbandingan antara panjang sisi-sisi dalam sebuah segitiga.
Misalnya, di segitiga siku-siku, sin didefinisikan sebagai perbandingan sisi depan sudut terhadap sisi miring. Cos adalah perbandingan sisi samping terhadap sisi miring. Sedangkan tan menjadi perbandingan sisi depan terhadap sisi samping.
Memahami Dasar-dasar Trigonometri
Untuk dapat menggunakan trigonometri, kamu perlu mengenal beberapa rumus dasar yang sering muncul. Salah satu rumus populer tersebut adalah identitas trigonometri yang menyatakan bahwa sin²θ ditambah cos²θ selalu bernilai 1. Rumus ini menjadi dasar banyak turunan lainnya.
Ada juga hubungan antara tan dan secan, yakni 1 + tan²θ = sec²θ. Demikian pula antara cotangen dan cosecan: 1 + cot²θ = csc²θ. Meskipun terlihat rumit di awal, semua rumus saling berhubungan. Sehingga akan lebih mudah kita pahami jika sudah terbiasa menggunakannya dalam soal.
Selain itu, kita juga akan menjumpai rumus-rumus sudut ganda. Seperti sin(2θ) yang bernilai 2 sin θ cos θ, atau cos(2θ) yang setara dengan cos² θ dikurangi sin² θ. Ada juga rumus sudut setengah yang sering hadir dalam soal-soal lanjutan.
Sudut Istimewa dan Nilai Fungsi Trigonometri
Dalam trigonometri, terdapat beberapa sudut yang disebut sebagai sudut istimewa, seperti 0°, 30°, 45°, 60°, dan 90°. Untuk setiap sudut tersebut, nilai dari sin, cos, dan tan sudah pasti dan sering digunakan dalam berbagai soal.
Misalnya, sin 30° bernilai 0,5, sementara tan 45° bernilai 1. Menghafalkan nilai-nilai ini sangat disarankan karena bisa mempercepat pengerjaan soal-soal tanpa perlu menghitung manual.
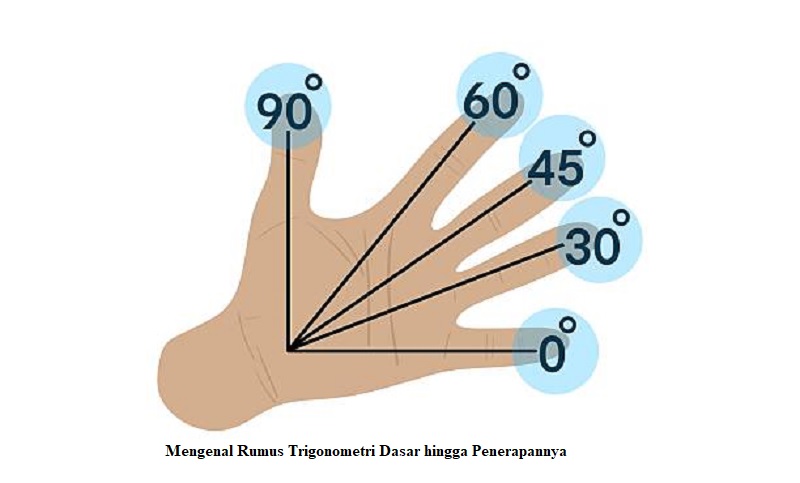
Menurut video Short @Vincdels, ada teknik menarik menggunakan telapak tangan kiri yang bisa membantu menghitung nilai sin, cos, dan tan. Khususnya untuk sudut istimewa 0°, 30°, 45°, 60°, dan 90°.
Caranya cukup sederhana dan praktis: buka telapak tanganmu menghadap ke depan, lalu bayangkan ibu jari sebagai sudut 90°, jari telunjuk 60°, jari tengah 45°, jari manis 30°, dan kelingking 0°.
Untuk mendapatkan nilai sinus, hitung jumlah jari di sebelah kanan jari yang mewakili sudut itu, lalu gunakan rumus akar dari jumlah jari dibagi 2.
Misalnya, untuk sin 30°, lipat jari manis (yang mewakili 30°). Di bawah jari tersebut ada satu jari (kelingking), maka sin 30° = akar dari 1 dibagi 2, yaitu 1/2.
Sementara untuk menghitung nilai cosinus (cos), masih menggunakan metode yang sama, hanya saja kita hitung jumlah jari di sisi kanan (bagian atas dari jari yang dilipat). Contohnya, untuk cos 60°, kita lipat jari telunjuk (yang mewakili 60°). Di atas jari itu ada satu jari (ibu jari), jadi cos 60° = akar dari 1 dibagi 2 = 1/2.
Untuk nilai tangen (tan), cukup membagi nilai sin dengan nilai cos dari sudut tersebut. Teknik sederhana ini sangat berguna saat mengerjakan soal matematika. Khususnya ketika perlu nilai-nilai sin, cos, atau tan dari sudut istimewa tanpa menggunakan kalkulator atau tabel.
Penerapan Trigonometri dalam Kehidupan Nyata
Walaupun sering dianggap hanya berlaku di ruang kelas, rumus trigonometri ternyata memiliki banyak kegunaan di dunia nyata. Dalam dunia konstruksi misalnya, trigonometri berfungsi untuk menghitung kemiringan atap bangunan atau panjang tangga.
Dalam astronomi, ilmuwan menggunakannya untuk mengukur jarak antar planet atau benda langit berdasarkan sudut pengamatan dari bumi. Begitu pula dalam navigasi dan sistem GPS. Trigonometri membantu sistem menghitung posisi dan jarak secara presisi.
Menguasai rumus trigonometri tidak hanya penting untuk menyelesaikan soal-soal matematika. Tetapi juga menjadi bekal dalam banyak bidang praktis di kehidupan. Dengan memahami fungsi dasar seperti sin, cos, dan tan, serta berlatih menyelesaikan soal secara rutin, maka akan semakin terbiasa dan percaya diri. Belajar dengan cara yang tepat membuat trigonometri terasa jauh lebih mudah dan menyenangkan. /Edit



